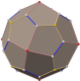
Catalan solid

Set of Catalan solids

The rhombic dodecahedron's construction, the dual polyhedron of a cuboctahedron, by Dorman Luke construction

The Catalan solids are the dual polyhedron of Archimedean solids, a set of thirteen polyhedrons with highly symmetric forms semiregular polyhedrons in which two or more polygonal of their faces are met at a vertex. A polyhedron can have a dual by corresponding vertices to the faces of the other polyhedron, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. One way to construct the Catalan solids is by using the method of Dorman Luke construction.

These solids are face-transitive or isohedral because their faces are transitive to one another, but they are not vertex-transitive because their vertices are not transitive to one another. Their dual, the Archimedean solids, are vertex-transitive but not face-transitive. Each has constant dihedral angles, meaning the angle between any two adjacent faces is the same. Additionally, both Catalan solids rhombic dodecahedron and rhombic triacontahedron are edge-transitive, meaning there is an isometry between any two edges preserving the symmetry of the whole. These solids were also already discovered by Johannes Kepler during the study of zonohedrons, until Eugene Catalan first completed the list of the thirteen solids in 1865.

The pentagonal icositetrahedron and the pentagonal hexecontahedron are chiral because they are dual to the snub cube and snub dodecahedron respectively, which are chiral; that is, these two solids are not their own mirror images.

Eleven of the thirteen Catalan solids are known to have the Rupert property (a copy of the same solid can be passed through a hole in the solid).

The thirteen Catalan solids

Name	Image	Faces	Edges	Vertices	Dihedral angle	Point group
triakis tetrahedron		12 isosceles triangles	18	8	129.521°	Td
rhombic dodecahedron		12 rhombi	24	14	120°	Oh
triakis octahedron		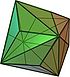24 isosceles triangles	36	14	147.350°	Oh
tetrakis hexahedron		24 isosceles triangles	36	14	143.130°	Oh
deltoidal icositetrahedron		24 kites	48	26	138.118°	Oh
disdyakis dodecahedron		48 scalene triangles	72	26	155.082°	Oh
pentagonal icositetrahedron		24 pentagons	60	38	136.309°	O
rhombic triacontahedron		30 rhombi	60	32	144°	Ih
triakis icosahedron		60 isosceles triangles	90	32	160.613°	Ih
pentakis dodecahedron		60 isosceles triangles	90	32	156.719°	Ih
deltoidal hexecontahedron		60 kites	120	62	154.121°	Ih
disdyakis triacontahedron		120 scalene triangles	180	62	164.888°	Ih
pentagonal hexecontahedron		60 pentagons	150	92	153.179°	I

References

Works cited

• Cundy, H. Martyn; Rollett, A. P. (1961), Mathematical Models (2nd ed.), Oxford: Clarendon Press, MR 0124167.
• Diudea, M. V. (2018), Multi-shell Polyhedral Clusters, Carbon Materials: Chemistry and Physics, vol. 10, Springer, doi:10.1007/978-3-319-64123-2, ISBN 978-3-319-64123-2.
• Fredriksson, Albin (2024), "Optimizing for the Rupert property", The American Mathematical Monthly, 131 (3): 255–261, arXiv:2210.00601, doi:10.1080/00029890.2023.2285200.
• Gailiunas, P.; Sharp, J. (2005), "Duality of polyhedra", International Journal of Mathematical Education in Science and Technology, 36 (6): 617–642, doi:10.1080/00207390500064049, S2CID 120818796.
• Heil, E.; Martini, H. (1993), "Special convex bodies", in Gruber, P. M.; Wills, J. M. (eds.), Handbook of Convex Geometry, North Holland, ISBN 978-0-08-093439-6
• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)

External links

• Weisstein, Eric W. "Catalan Solids". MathWorld.
• Weisstein, Eric W. "Isohedron". MathWorld.
• Catalan Solids – at Visual Polyhedra
• Archimedean duals – at Virtual Reality Polyhedra
• Interactive Catalan Solid in Java
• Download link for Catalan's original 1865 publication – with beautiful figures, PDF format